Yonedaについて
2015/3/24 モナド基礎勉強会
by ちゅーん(@its_out_of_tune)
自己紹介
自己紹介
- 野生のHaskller(27♂)
- 東京都近郊に生息・現NEET
- クルージング(スケボー)
- SOUND VOLTEX(音ゲー)
- リトルノア(スマフォゲー)
- ゆずこ(ゆゆ式)可愛い
- ヲ級ちゃん可愛い
- 艦これやってない
HN: ちゅーん
Twitter:
@its_out_of_tune
Github:
tokiwoousaka
自己紹介
- Takahashi Monad:
スライド作成用のHaskell言語内DSL
このスライドもこれで作成しました - Sarasvati:
オーディオインターフェイス
PortAudioのラッパーのラッパーとして開発中
はじめに
はじめに
焼き肉が食べたい
はじめに
はじめに
はじめに
はじめに
というわけで
はじめに
本日のテーマ
Yoneda
はじめに
どうしてこうなった
はじめに
なお、そのような事情により、
本日はモナドの基礎の話はできませんが、
まぁ、某ボドゲ大会で、ある方が
「米田の補題は基礎だから」
って言っていたので、基礎繋がりで、
良いんじゃないかと思います。
米田の補題
米田の補題
- 米田信夫(1930-1996)
- 日本の数学者/計算機科学者
- 1961年 東京大学 理学博士
- ALGOLに関する功績
- 圏論における米田の補題
- ソースはWikipedia☆(ゝω・)v

※肖像画は檜山正幸さんのブログよりお借りしました
米田の補題
以下の全単射の存在を示す定理
米田関手(後述)と呼ばれる関手が充満忠実である事を証明する
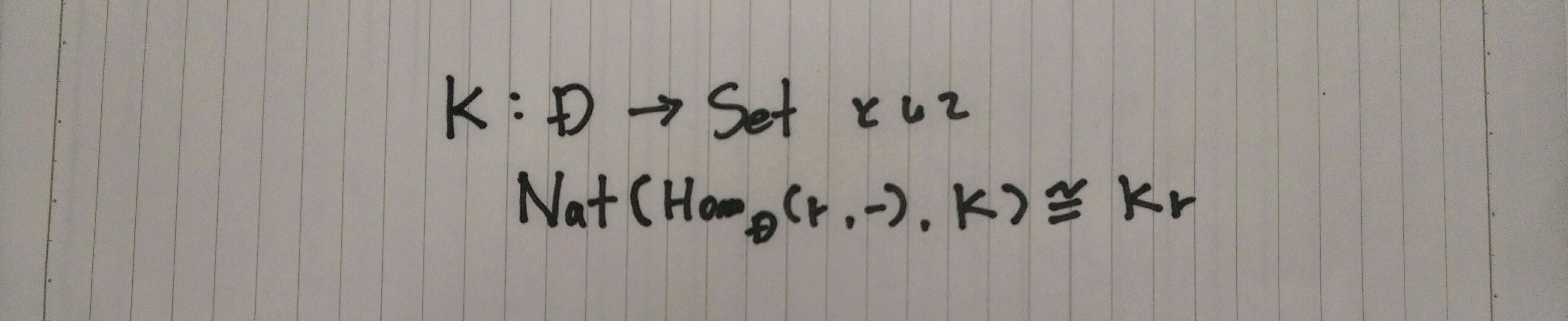
米田の補題
マックレーン「圏論の基礎」による証明
「以下の可換図式によって示される」
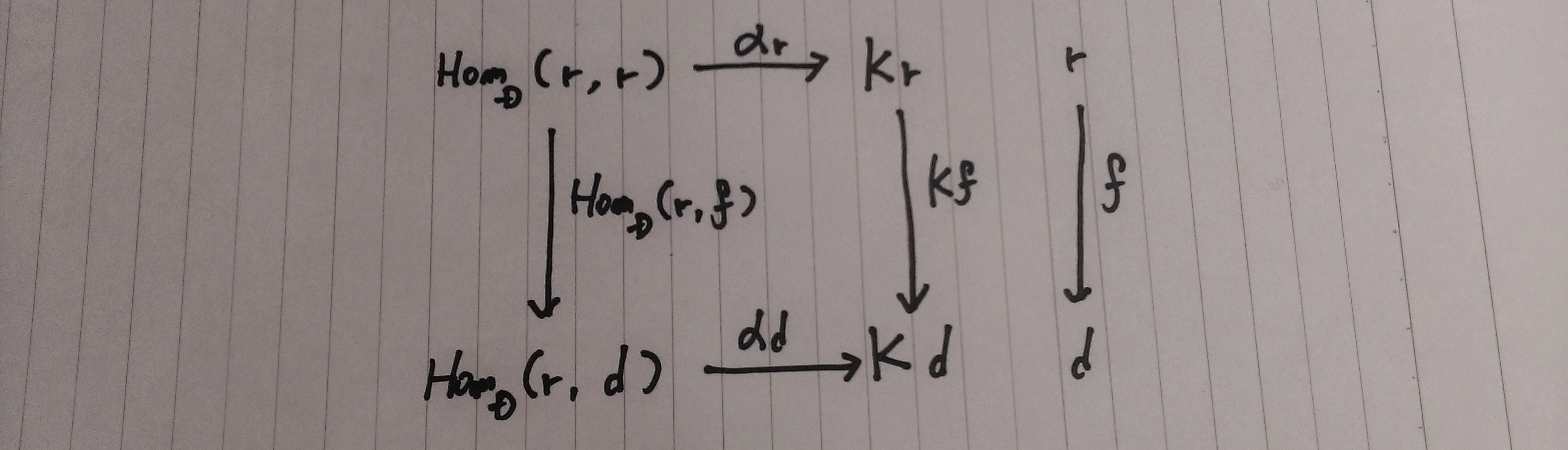
米田の補題
なるほどわからん
米田の補題
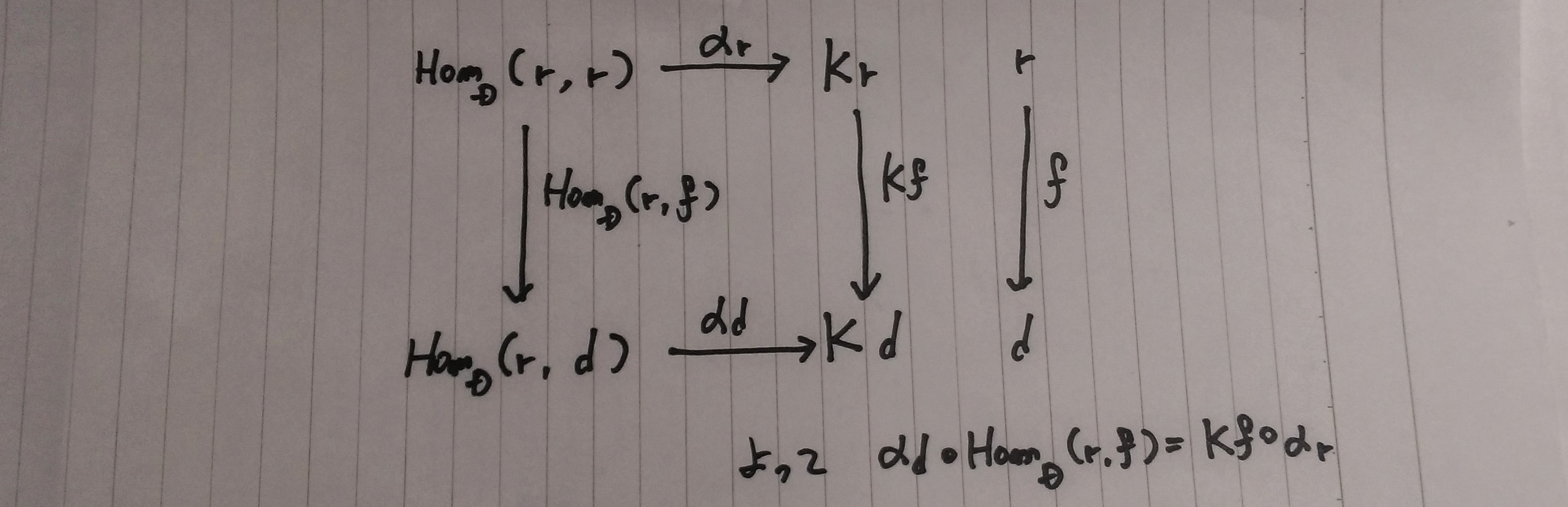
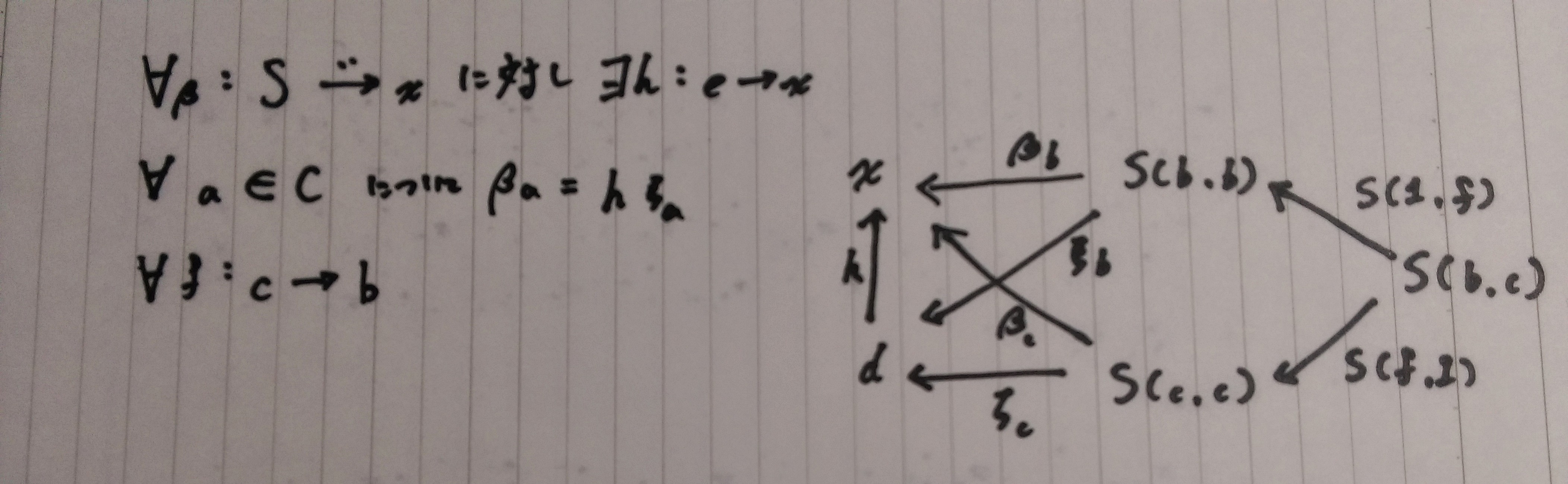
米田の補題の証明には、以下の前提が必要
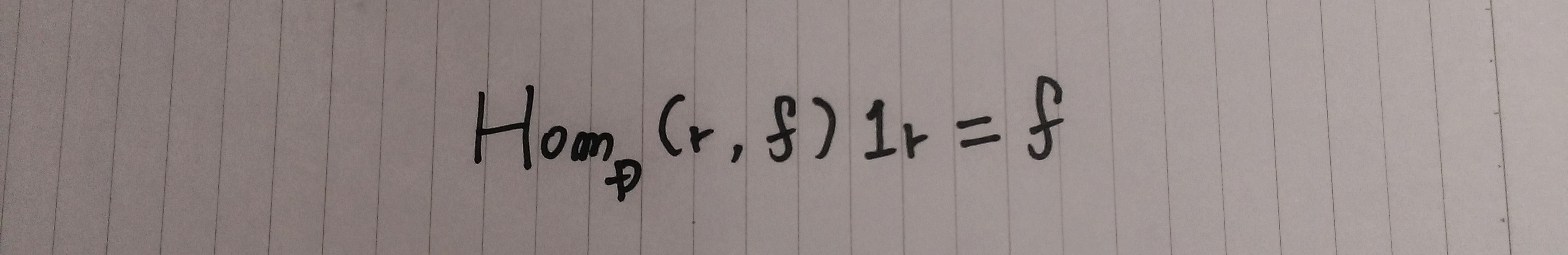
米田の補題
米田の補題
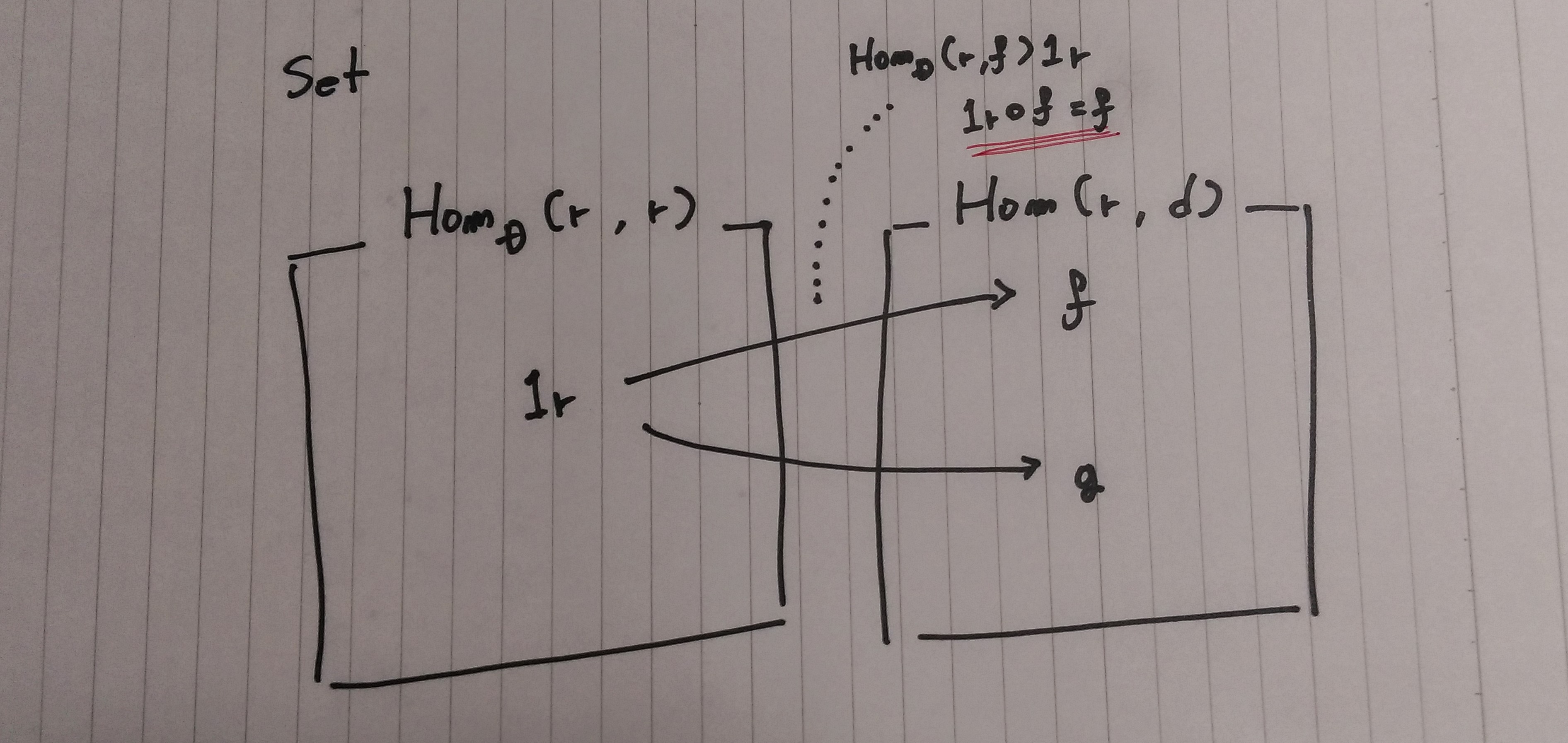
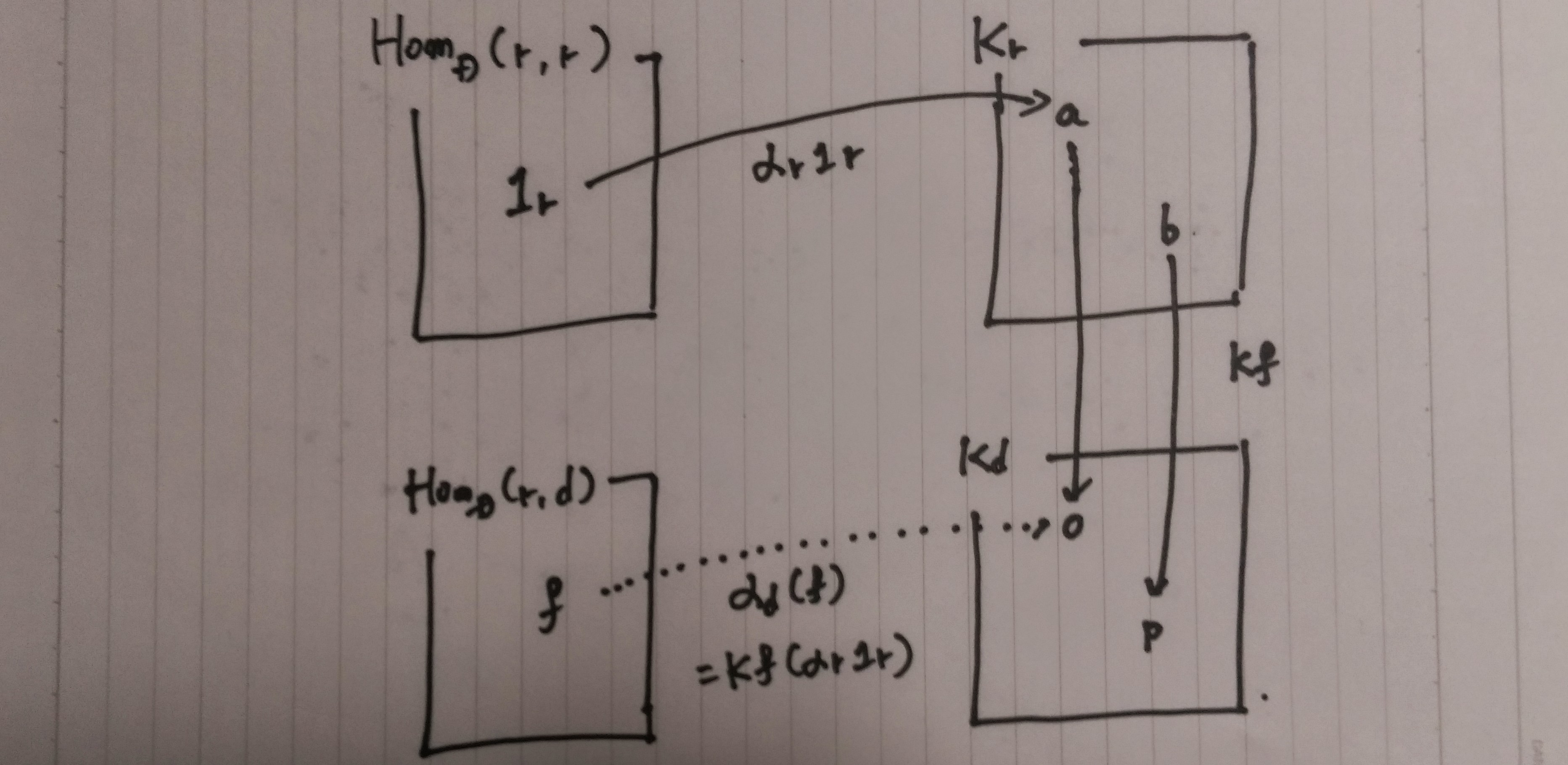
αは自然変換なので
「圏論の基礎」で示されていた以下の図式は可換
米田の補題
左辺に1rを作用
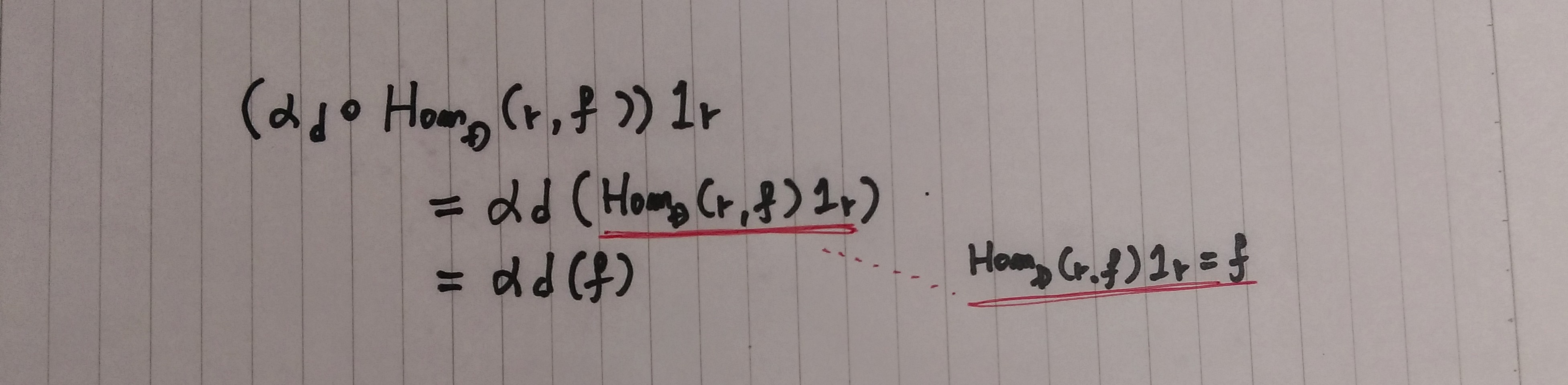
米田の補題
右辺に1rを作用
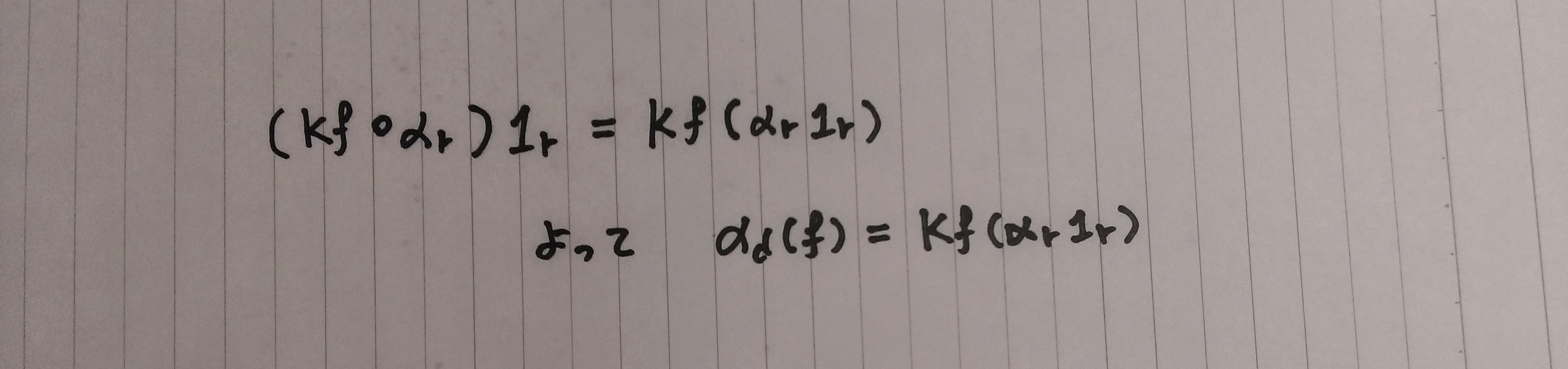
米田の補題
αd(f)=Kf(αr1r)は∀f:r->dで成り立つ
よってαr1rが定まればαが定まる
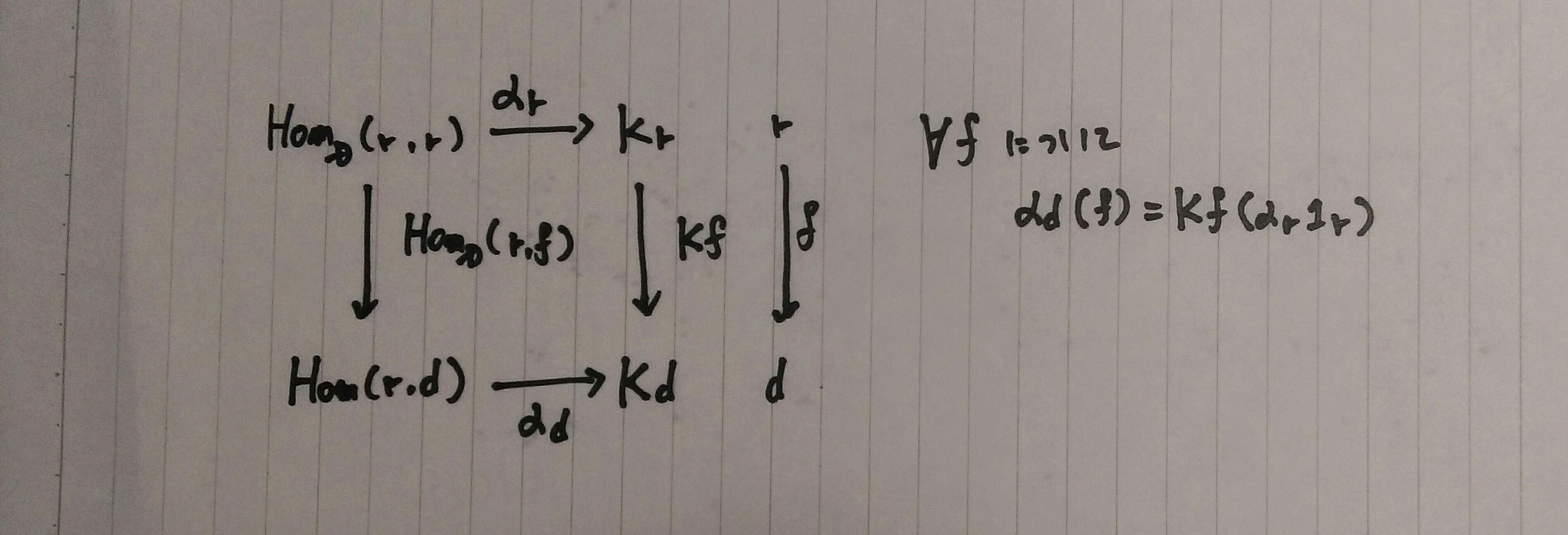
米田の補題
逆に、αが定まればαr1rも定まる
得られたαrに1rを作用させれば良いだけなので自明
米田の補題
αとαr1rは、米田の補題の左辺と右辺
ここまでの説明は片方の集合から
もう片方が完全に定まる事を示していた
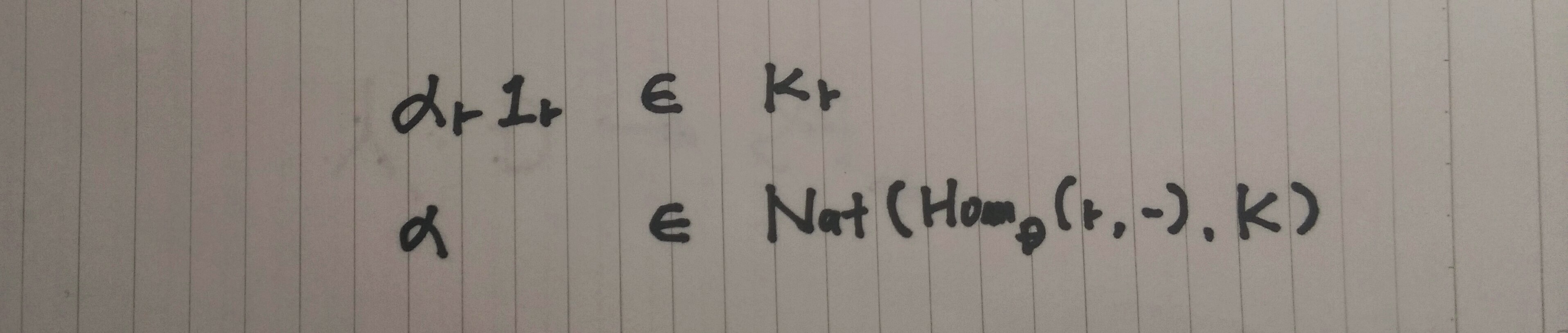
米田の補題
米田の補題
よって、以下の集合間に全単射が存在する事が証明される
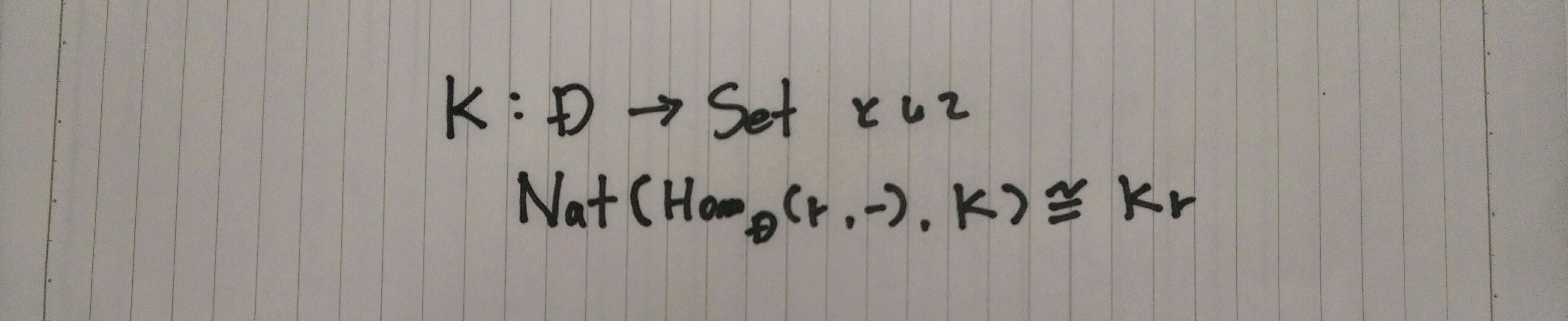
米田の補題
この補題は、以下のように定義された
米田関手が充満忠実である事を証明する
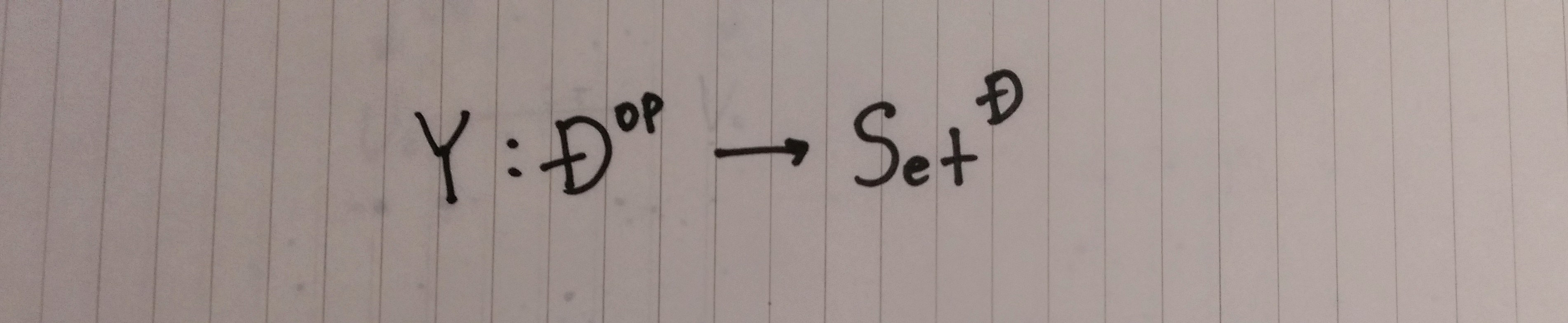
米田の補題
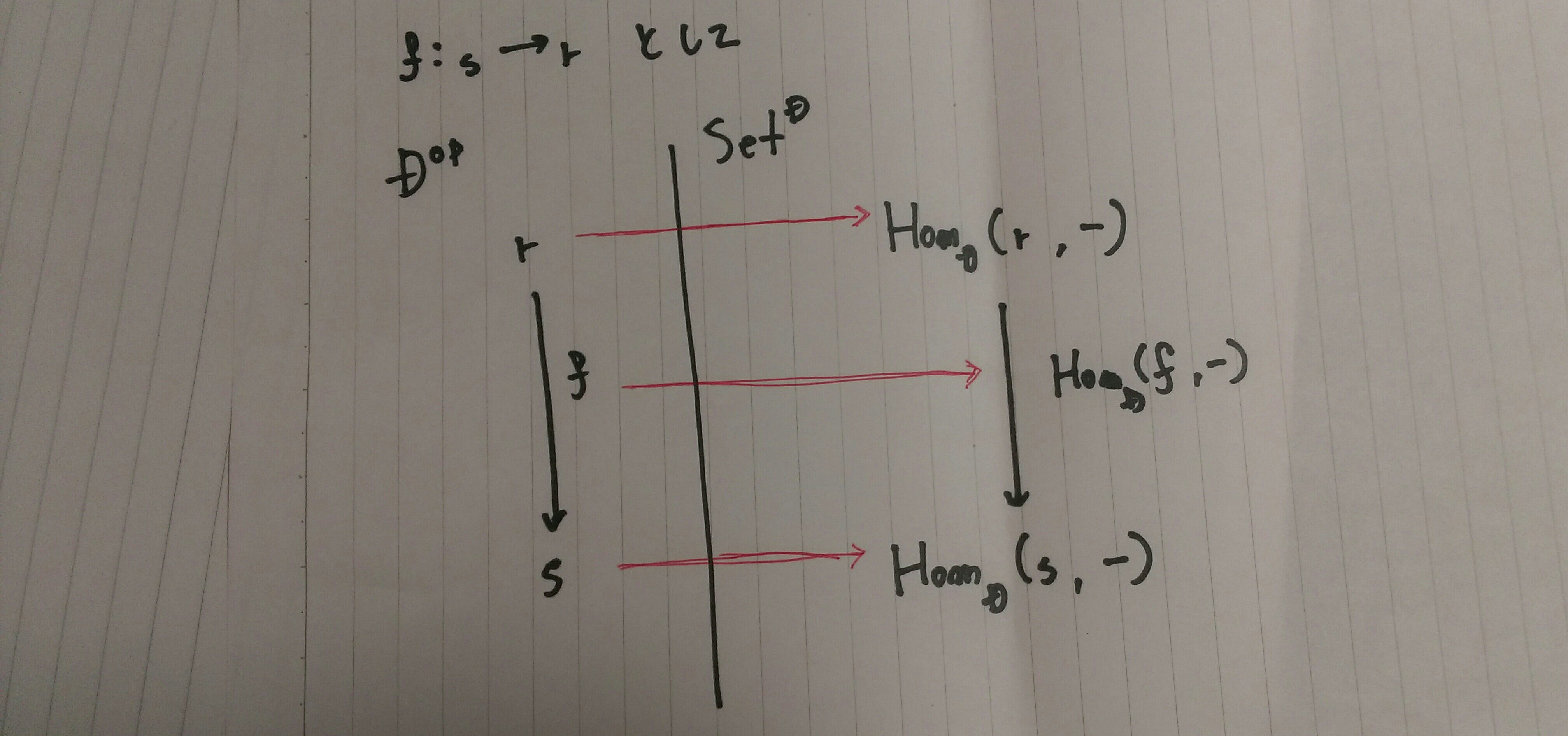
米田の補題

米田の補題
米田関手の双対として、
米田埋め込みという充満忠実な関手がある。
これは任意の圏をSetに移せるため有用・・・だそうだ。

HaskellとYoneda
HaskellとYoneda
米田の補題の全単射の左辺を
Haskellのコードに落としこむ
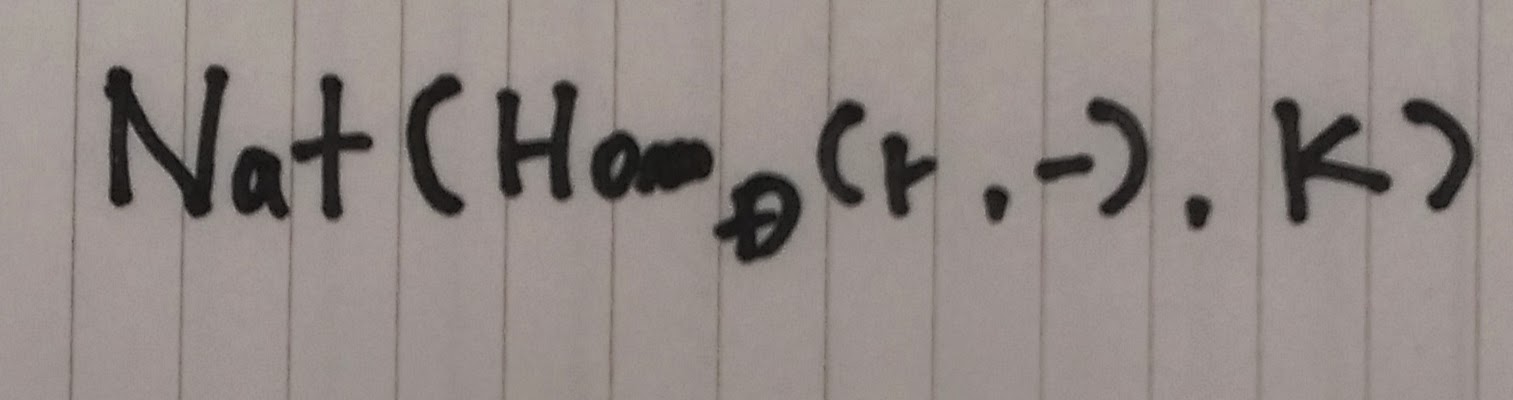
newtype Yoneda f x
= Yoneda { runYoneda :: forall b. (x -> b) -> f b }
HaskellとYoneda
Yoneda型は以下のようにしてFunctorにすることで、
米田の補題により、任意のFunctor f と同値になる。
instance Functor (Yoneda f) where
fmap f (Yoneda m) = Yoneda $ \k -> m (k . f)
たとえば、Yoneda Maybe a は
Functorとして完全に Maybe a 型に代用する事が出来る。
HaskellとYoneda
Yoneda型が任意のFunctorの代用になる事を確認するため、
簡単な関数を定義しておこう。
lowerYoneda :: Yoneda f a -> f a
lowerYoneda (Yoneda m) = m id
liftYoneda :: Functor f => f a -> Yoneda f a
liftYoneda v = Yoneda $ \k -> fmap k v
HaskellとYoneda
その上で、以下のコードを実行する事で
Yoneda型を仲介しても結果は変わらない事が確認できる。
ndigits :: Functor f => f Int -> f Int
ndigits = fmap length . fmap show
main :: IO ()
main = do
-- Just 114514
print . ndigits $ Just 114514
print . lowerYoneda . ndigits . liftYoneda $ Just 114514
-- Nothing
print . ndigits $ Nothing
print . lowerYoneda . ndigits . liftYoneda $ Nothing
HaskellとYoneda
Yoneda型を構成する際にmapの計算を組み込めれば、
元になる型がFunctorのインスタンスになっている必要はない。
関手が存在するかどうかは、型そのものの性質だからである。
data MyMaybe a = MyJust a | MyNothing
deriving (Show, Read, Eq, Ord)
yonedaMM :: MyMaybe a -> Yoneda MyMaybe a
yonedaMM (MyJust x) = Yoneda $ \k -> MyJust (k x)
yonedaMM MyNothing = Yoneda $ \_ -> MyNothing
main :: IO ()
main = do
print . lowerYoneda . fmap (*2) . yonedaMM $ MyJust 114514
print . lowerYoneda . fmap (*2) . yonedaMM $ MyNothing
HaskellとYoneda
改めて、Yonedaのfmapの実装を見てみよう。
mapした際に行われるのは基本的に関数操作である。
instance Functor (Yoneda f) where
fmap f (Yoneda m) = Yoneda $ \k -> m (k . f)
データへの直接的な操作はオーバーヘッドになり兼ねない。
つまりYonedaは、Functorに対する大きな操作の、
パフォーマンス対策ツールになり得る。
Yonedaの双対CoYoneda
Yonedaの双対CoYoneda
米田の補題の双対として「余米田の補題」があり、
余米田の補題は、以下のようにHaskell上で実装される。
data CoYoneda f x = forall b. CoYoneda (b -> x) (f b)
instance Functor (CoYoneda f) where
fmap f (CoYoneda g v) = CoYoneda (f . g) v
Yonedaの双対CoYoneda
CoYonedaは概ね、Yonedaと同等の機能を持つ。
liftCoYoneda :: f a -> CoYoneda f a
liftCoYoneda = CoYoneda id
lowerCoYoneda :: Functor f => CoYoneda f a -> f a
lowerCoYoneda (CoYoneda f x) = fmap f x
main :: IO ()
main = do
print . lowerCoYoneda . ndigits . liftCoYoneda $ Just 114514
print . lowerCoYoneda . ndigits . liftCoYoneda $ Nothing
Yonedaの双対CoYoneda
YonedaとCoYonedaの双対性は、
lift, lower関数の型定義に明確に現れる。
liftYoneda :: Functor f => f a -> Yoneda f a
liftCoYoneda :: f a -> CoYoneda f a
lowerYoneda :: Yoneda f a -> f a
lowerCoYoneda :: Functor f => CoYoneda f a -> f a
Yonedaはliftの際にmap操作が決定しなくてはいけない、
対して、CoYonedaはlowerで決定する。
Yonedaの双対CoYoneda
Yonedaの場合と同様、lowerの際にmapの計算を組み込めれば、
その型自体がFunctorのインスタンスである必要はない。
coyonedaMM :: CoYoneda MyMaybe a -> MyMaybe a
coyonedaMM (CoYoneda f (MyJust x)) = MyJust $ f x
coyonedaMM (CoYoneda _ _) = MyNothing
main :: IO ()
main = do
print . coyonedaMM . fmap (*2) . liftCoYoneda $ MyJust 114514
print . coyonedaMM . fmap (*2) . liftCoYoneda $ MyNothing
余米田の補題
余米田の補題
お詫び
余米田の補題
米田の補題の双対
余米田の補題
余米田の補題
余米田の補題
時間的都合と
余米田の補題
実力不足により
余米田の補題
理解しきれなかった
orz orz orz
余米田の補題
今日は
調べて来た事をそのまんま
余米田の補題
垂れ流します
(`・ω・´)ゞ
余米田の補題
対角自然変換(くさび)とは、
以下の割り当てを行う関数の事である。
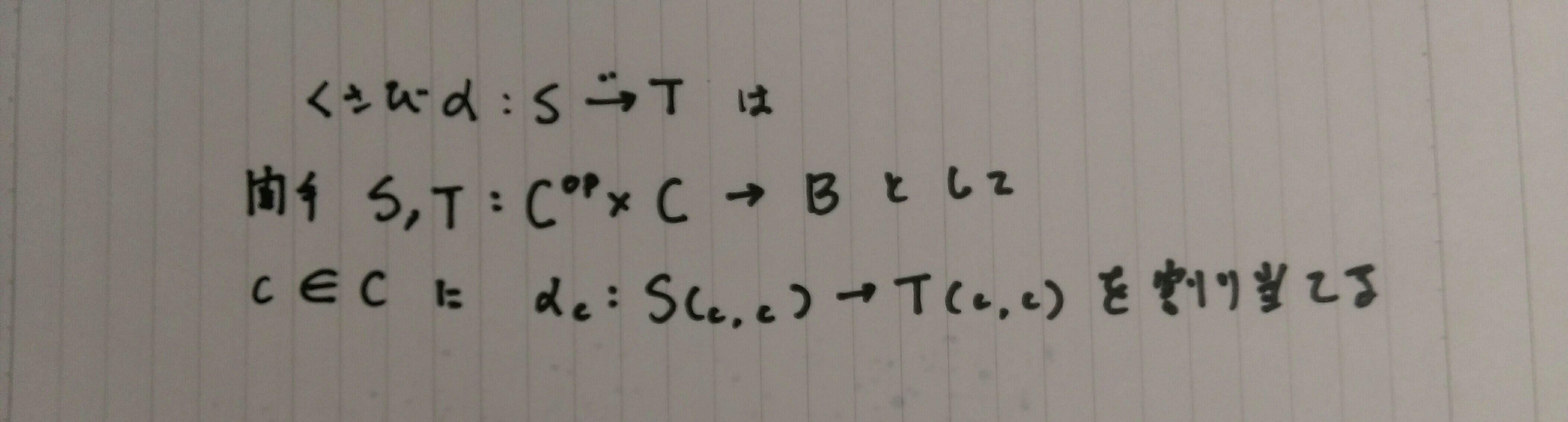
余米田の補題
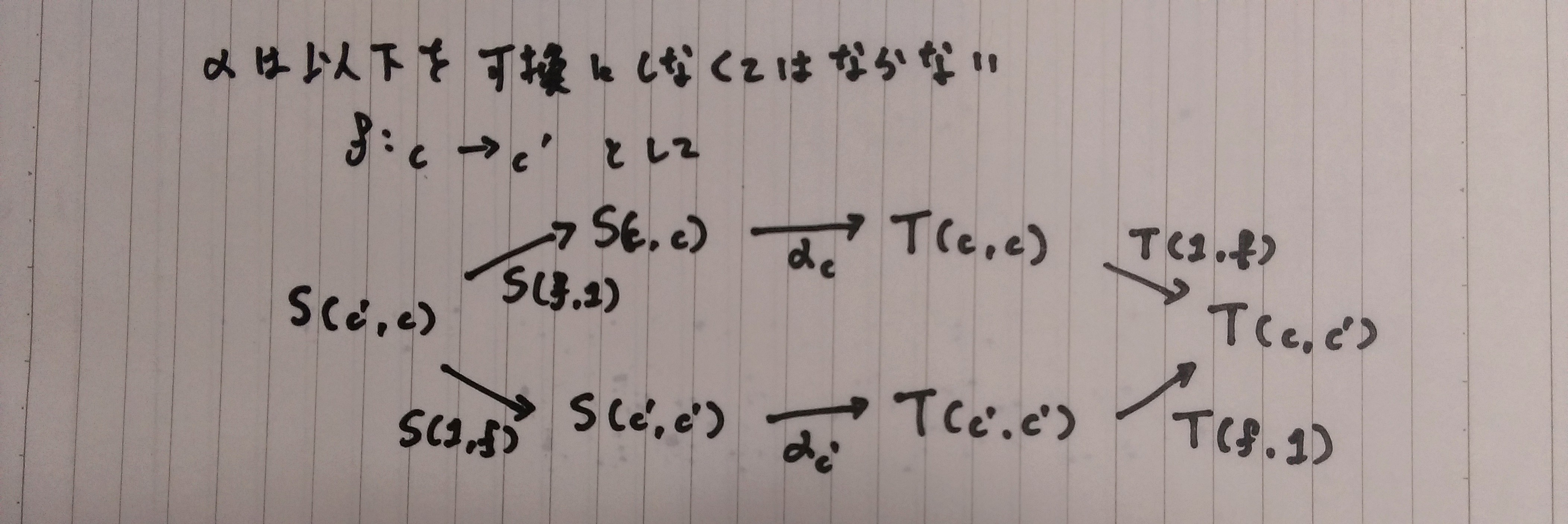
余米田の補題
エンドとは、あるe:Xと、くさびω:e->Sの組であり、
以下の規則を満たし、図式を可換にするもの。
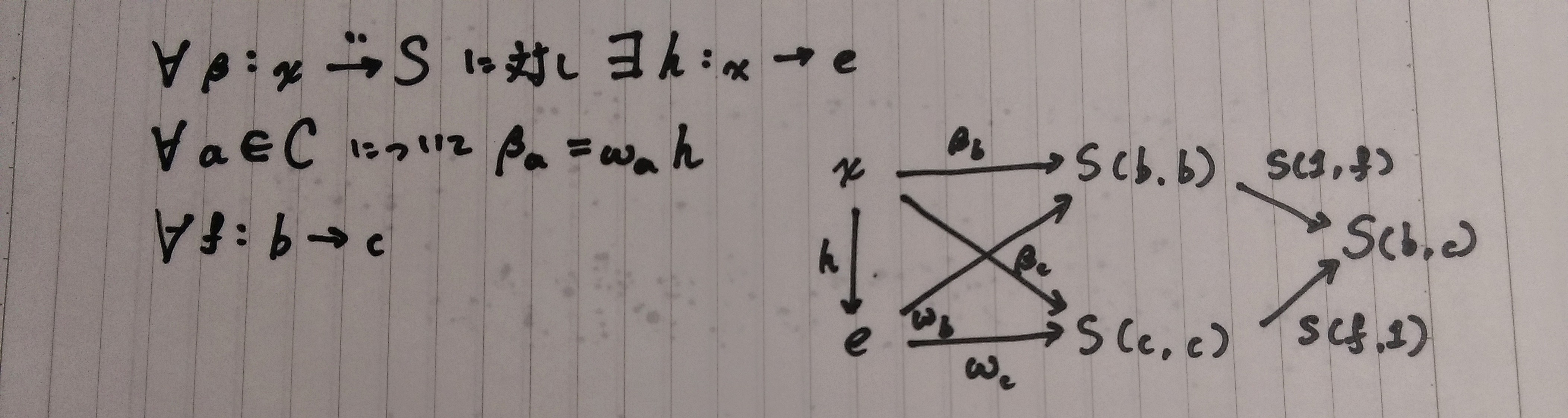
余米田の補題
また、エンドの対象e自体も述語の汎用でエンドと呼ばれ、
積分記号を用いて以下のように記述される。
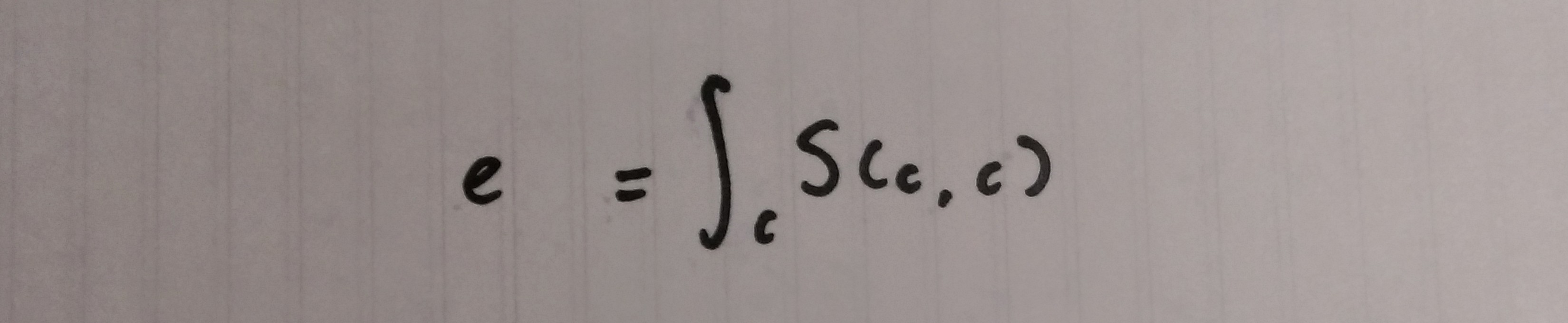
余米田の補題
エンドの双対コエンドは、
あるd:Xと、くさびζ:d->Sの組であり、
余米田の補題
エンドと同様、d自体もコエンドと呼ばれ、
積分記号を用いて以下のように記述される。
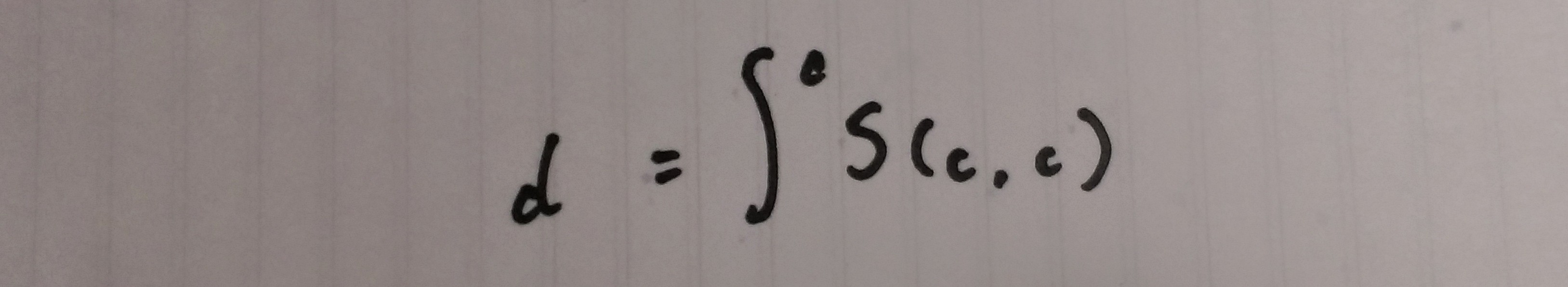
余米田の補題
米田の補題はエンドを用いて、
以下のように定義する事も可能で・・・
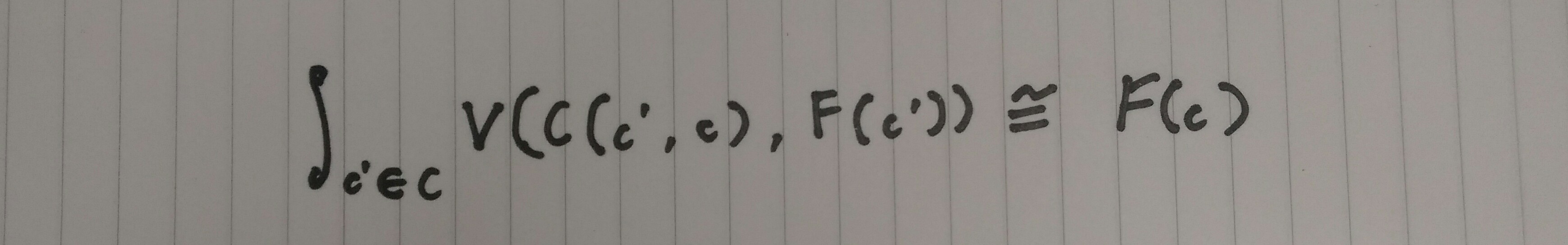
余米田の補題
余米田の補題はコエンドを用いて、
以下のように定義される・・・のだそうだ。

余米田の補題
誰か詳しく教えて下さい
(´・ω・`)
Freeモナド
Freeモナド
Freeと呼ばれる型は以下のように定義され、
FunctorおよびMonadのインスタンスとなる
data Free f r = Free (f (Free f r)) | Pure r
instance Functor f => Functor (Free f) where
fmap f x = x >>= return . f
instance Functor f => Monad (Free f) where
return = Pure
Free x >>= f = Free $ fmap (>>= f) x
Pure x >>= f = f x
Freeモナド
liftF関数を使い
Functorインスタンスのデータコンストラクタを元に、
Freeモナドのモナドアクションを生成できる。
liftF :: Functor f => f r -> Free f r
liftF cmd = Free (fmap Pure cmd)
-----
just :: a -> Free Maybe a
just = liftF . Just
nothing :: Free Maybe a
nothing = liftF Nothing
Freeモナド
このようにして作成されたFree Maybeモナドは
実質的に、Freeモナドと同様に記述する事ができ・・・
sample1 :: Free Maybe Int
sample1 = do
x <- just 10
y <- just 20
return $ x + y
sample2 :: Free Maybe Int
sample2 = do
x <- just 10
y <- nothing
return $ x + y
Freeモナド
retract関数を使い、
Maybeモナドと同様の結果を得る事が出来る。
main :: IO ()
main = do
print . retract $ sample1 -- Just 30
print . retract $ sample2 -- Nothing
このように、Freeモナドは任意のモナドの代用となる。
Freeモナド
liftF関数は任意のFunctorを元に、
Freeのモナドアクションを生成する。
data MyMaybe a = MyJust a | MyNothing
deriving (Show, Read, Eq, Ord, Functor)
just :: a -> Free MyMaybe a
just = liftF . MyJust
nothing :: Free MyMaybe a
nothing = liftF MyNothing
Freeモナド
Freeから内包した型を引き剥がす関数を定義できれば、
その型がMonad型クラスのインスタンスである必要はない。
runFreeMaybe :: Free MyMaybe a -> MyMaybe a
runFreeMaybe (Free (MyJust x)) = runFreeMaybe x
runFreeMaybe (Free _) = MyNothing
runFreeMaybe (Pure a) = MyJust a
これはYonedaがそうであったように、
Monadの存在は、ある型の性質に過ぎないからである。
Operationalモナド
Operationalモナド
- liftF関数はFunctorインスタンスのデータを元に
Freeモナドのモナドアクションを生成する - Freeモナドは任意のFunctorをモナドにすると解釈できる
- Free f a からFreeを引き剥がす際に
f a のモナドとしての働きが決定する - CoYonedaは任意の型を内包して、Functorとして機能する
- CoYonedaは任意のデータ型をFunctorにすると解釈できる
- CoYoneda f a から CoYonedaを引き剥がす際に
f a のFunctorとしての働きが決定する
Operationalモナド
FreeとCoYoneda、二つを組み合わせて、
任意の型を一気にMonadとして扱えるようにする。
これが、Operationalモナドの基本的なアイディアである。
newtype Program f a
= Program { toFree :: Free (CoYoneda f) a }
instance Monad (Program f) where
return = Program . return
x >>= f = Program $ toFree x >>= toFree . f
Operationalモナド
Operationalを利用してDSLを作成する場合、
まず最初にGADTsを用いて必要なAPIを羅列する。
ここでProgram型と組み合わせたtype宣言をしておくと良い。
data IntIOBase a where
PutInt :: Int -> IntIOBase ()
GetInt :: IntIOBase Int
PrintInt :: IntIOBase ()
type IntIO = Program IntIOBase
Operationalモナド
データコンストラクタをモナドアクションにするには、
singleton関数を利用すると良い。
singleton :: f a -> Program f a
singleton = Program . liftF . liftCoYoneda
putInt :: Int -> IntIO ()
putInt = singleton . PutInt
getInt :: IntIO Int
getInt = singleton GetInt
printInt :: IntIO ()
printInt = singleton PrintInt
Operationalモナド
各アクションが具体的に何を行うか、まだ指定していない。
しかし、Program型はモナドなので、この時点でdo記法によって、
プログラムを記述する事が可能になっている。
sample :: IntIO ()
sample = do
printInt
putInt 100
printInt
putInt 200
printInt
Operationalモナド
DSLを実行する関数の構築には、interpret関数を用いると良い。
第一引数には、
DSLを他の具体的なモナドに翻訳する関数を指定する。
interpret :: forall instr m b. Monad m =>
(forall a. instr a -> m a) -> Program instr b -> m b
interpret g (Program (Free (CoYoneda f x)))
= g x >>= interpret g . Program . f
interpret _ (Program (Pure a)) = return a
Operationalモナド
以下は、interpret関数の具体的な使用例である。
runIntIO :: IntIO a -> Int -> IO a
runIntIO t i = evalStateT (interpret advent t) i
where
advent :: IntIOBase a -> StateT Int IO a
advent (PutInt x) = put x
advent GetInt = get
advent PrintInt = get >>= liftIO . print
Operationalモナド
- モナドを作るのはややこしい
(モナド則、Applicativeとの兼ね合い) - モナドを言語内DSLを作るためのツールと考える
- 概ね モナドの設計=APIの策定
- 実装部分は切り離せたほうが良い
- Operationalは、APIを書き連ねる所から設計がはじまる
- Operationalなら、API設計と実装部分は完全に切り離す事ができる
→Operationalは言語内DSL開発の有用な選択肢になり得る
まとめ
まとめ
- 米田の補題。なんか凄い全単射が証明されている
- それをHaskellに落としこんだらYonedaになって便利っぽい
- Yonedaの双対はCoYonedaとかいうらしい
- YonedaもCoYonedaも好きな型をFunctorに出来る。すごい
- FreeモナドはFunctorをモナドに出来る。すごい
- FreeとCoYonedaを組み合わせると楽にモナドが作れて便利
- 米田先生すごい!イケメン!→結論