LensでHaskellを
もっと格好良く!
2015/5/30 Lens&Prism勉強会
by ちゅーん(@its_out_of_tune)
自己紹介
- 野生のHaskller(27♂)
- 東京都近郊に生息
- 休職中
- クルージング(スケボー)
- SOUND VOLTEX(音ゲー)
- リトルノア(スマフォゲー)
- ヲ級ちゃん可愛い
- 艦これやってない
HN: ちゅーん
Twitter:
@its_out_of_tune
Github:
tokiwoousaka
自己紹介
- Takahashi Monad:
スライド作成用の言語内DSL
拡張済み/複雑なスライドも作れる
本スライドもこれで作成
GHC7.10非対応 。゜。゜(ノД`)゜。゜。 - Sarasvati:
開発中のオーディオインターフェイス
PortAudioのラッパーのラッパー
HaskellのLens
HaskellのLens
2013/3/31 ekmett勉強会で、
Haskellのlensについて発表。
- 基本的な使い方
- 基本的な仕組みと実装
- 簡単な応用等
HaskellのLens
旧スライドでの発表
HaskellのLens
- ScalaのLensと実装が違う?
-> van Laarhoven lens - 考案者 van Laarhovenがブログ記事に
- Russell O'Connor証明等を論文に
- ekmett/lensはvan Laarhoven lensの拡張
- Haskellのlensはもっとすごいぞっ!
Opticから見たLens/Prism
2015/5/30 Lens&Prism勉強会
by ちゅーん(@its_out_of_tune)
Lensの限界
Lensの限界
Lensアクセッサを利用すれば、
複雑な構造へアクセスする事が出来る
(1, (2, 3, (4, 999)), 6)^._2._3._2 -- 999
(1, (2, 3, (4, 5)), 6)&_2._3._2.~999 -- (1, (2, 3, (4, 999)), 6)
Lensの限界
fooような構造から"999"を操作したい場合は?
barのような場合は?
let foo = (1, Left (999, 3), 4)
:: (Int, Either (Int, Int) String, Int)
let bar = (1, Right "Test", 4)
:: (Int, Either (Int, Int) String, Int)
Lensの限界
頑張ってlensだけでGetする
print $ case foo^._2 of
Left inner -> Just (inner^._1)
Right _ -> Nothing
print $ case bar^._2 of
Left inner -> Just (inner^._1)
Right _ -> Nothing
Lensの限界
(´゚д゚`)エー
Lensの限界
頑張ってlensだけでSetする
(_2%~(\case
Left x -> Left $ x&_1.~111
Right x -> Right x)) foo
(_2%~(\case
Left x -> Left $ x&_1.~111
Right x -> Right x)) bar
Lensの限界
。・゚・(ノ∀`)・゚・。
Lensの限界
lensは便利だけど
直和型が混ざると使えない
-> Primsを使おう!
Prismでパターンマッチ
Prismでパターンマッチ
Lensは直和型(Maybe, Either等)には使えない。
このような場合、
Prismという型を持つアクセッサを使う。
type Prism s t a b = ...
_Left :: Prism (Either a c) (Either b c) a b
_Right :: Prism (Either c a) (Either c b) a b
Prismでパターンマッチ
Prismを使った値の取得には(^?)を使う。
Maybe型を返し、値が取得できなかった場合、
結果はNothingとなる。
let left5 = Left 5 :: Either Int String
let rightHoge = Right "Hoge" :: Either Int String
left5^?_Left -- Just 5
left5^?_Right -- Nothing
rightHoge^?_Left -- Nothing
rightHoge^?_Right -- Just "Hoge"
Prismでパターンマッチ
Prismはマッチした場合のみ変更可能な、
Setterとして機能する。
left5&_Left.~999 -- Left 999
rightHoge&_Left.~999 -- Right "Hoge"
使い方はLensと同様
Prismでパターンマッチ
取得したい値がMonoidの場合に限り、(^.)が使える。
マッチ出来なかった場合の値はmemptyになる。
Just "hoge"^._Just -- OK "hoge"
Just 114514^._Just -- NG
Just (Sum 184)^._Just -- OK Sum { getSum = 184 }
(Nothing :: Maybe (Sum Int))^._Just -- OK Sum { getSum = 0 }
Prismでパターンマッチ
Prismはre関数を使う事によって、
データコンストラクタを被せるGetterになる。
値をSetする事は出来ない。
同様の事は、to関数を使っても実現可能。
print $ 100^.re _Just -- Just 100
print $ 100^.to Just -- Just 100
Prismでパターンマッチ
makePrisms関数を使えば、
独自の型に対してPrismアクセッサを作成できる。
data Foo a b = Hoge a | Piyo b | Fuga String
deriving (Show, Read, Eq, Ord)
makePrisms ''Foo
------ 以下のPrismが生成される ------
_Hoge :: Prism (Foo a c) (Foo b c) a b
_Piyo :: Prism (Foo c a) (Foo c b) a b
_Fuga :: Prism (Foo a b) (Foo a b) String String
Prismの合成
Prismの合成
PrismもLensと同様、関数合成によって合成可能。
let justLeft = Just (Left 5) :: Maybe (Either Int String)
let justRight = Just (Right "Hello") :: Maybe (Either Int String)
justLeft^?_Just._Left -- Just 5
justLeft^?_Just._Right -- Nothing
justRight^?_Just._Right -- Just "Hello"
justRight^._Just._Right -- "Hello"
Prismの合成
当然、PrismとLensを組み合わせても、
アクセッサとして利用可能。
let foo = (1, Left (999, 3), 4)
:: (Int, Either (Int, Int) String, Int)
let bar = (1, Right "Test", 4)
:: (Int, Either (Int, Int) String, Int)
print $ foo^?_2._Left._1 -- Just 999
print $ foo&_2._Left._1.~111 -- (1,Left (111,3),4)
print $ bar^?_2._Right -- Just "Test"
print $ bar^._2._Rightn -- "Test"
Prismの合成
Lensと合成した後はre関数が使えない。
合成したのがPrism同士ならば問題ない。
re (_Just._1) -- NG
(100^.re (_Just._Left)
:: Maybe (Either Int Int)) -- OK Just (Left 100)
Prismの合成
Prismの合成 -> re関数
Prismにre関数 -> 合成
では、結果の構造が逆になるため注意。
print $ (100^.re _Just.re _Left
:: Either (Maybe Int) Int) -- Left (Just 100)
print $ (100^.re (_Just._Left)
:: Maybe (Either Int Int)) -- Just (Left 100)
State上のPrism
State上のPrism
Lens同様、
MonadStateインスタンス上で状態へのSetが可能。
sample :: State (Int, Bool, Maybe (Int, String)) ()
sample = do
_1 .= 100
_3._Just._2 .= "Hello, Prism!"
return ()
State上のPrism
取り出したい値がモノイドならば
use関数を用いた値のGetが出来る。
sample :: State (Int, Bool, Maybe (Int, String)) String
sample = do
str <- use $ _3._Just._2
return str
State上のPrism
モノイドでない場合はpreuse関数を使う。
sampleState2 :: State (Int, Bool, Maybe (Int, String)) (Maybe Int)
sampleState2 = do
int <- preuse $ _3._Just._1
return int
State上のPrism
取得したい値がIntならば次のようにしても良い。
sample :: State (Int, Bool, Maybe (Int, String)) (Sum Int)
sample = do
int <- use $ _3._Just._1.to Sum
return int
色々なFunctor
色々なFunctor
Functorのイメージ:
実用上の認識に囚われない方が良い。
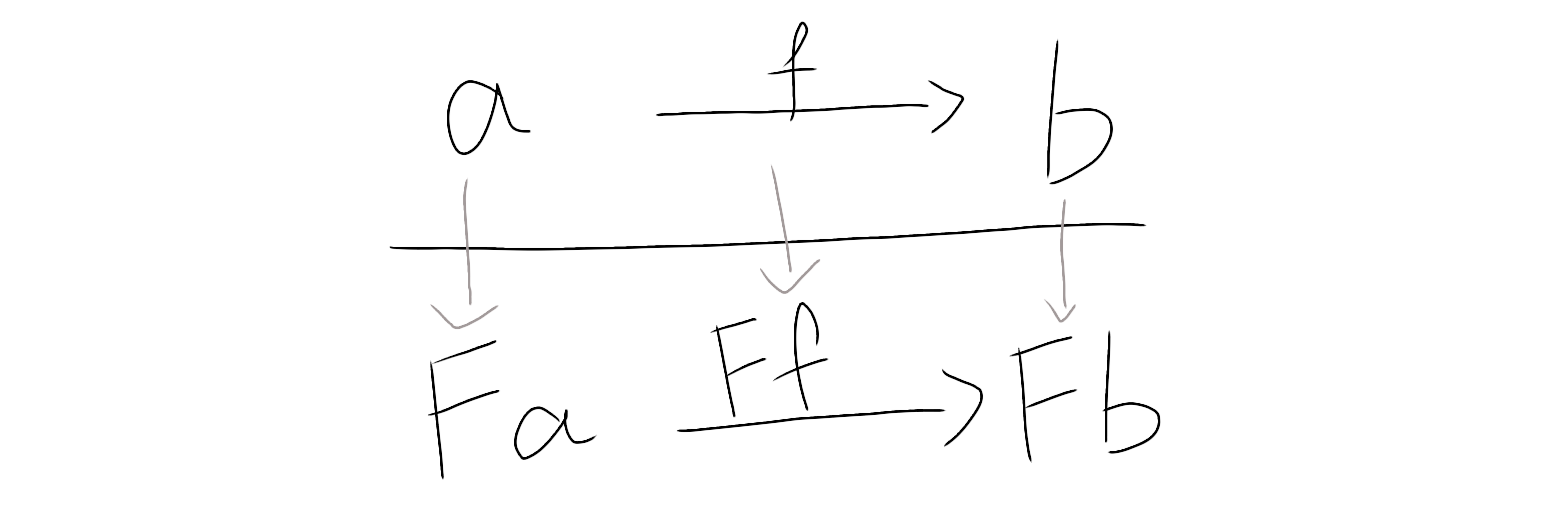
色々なFunctor
持ち上げ先の矢印を逆にする
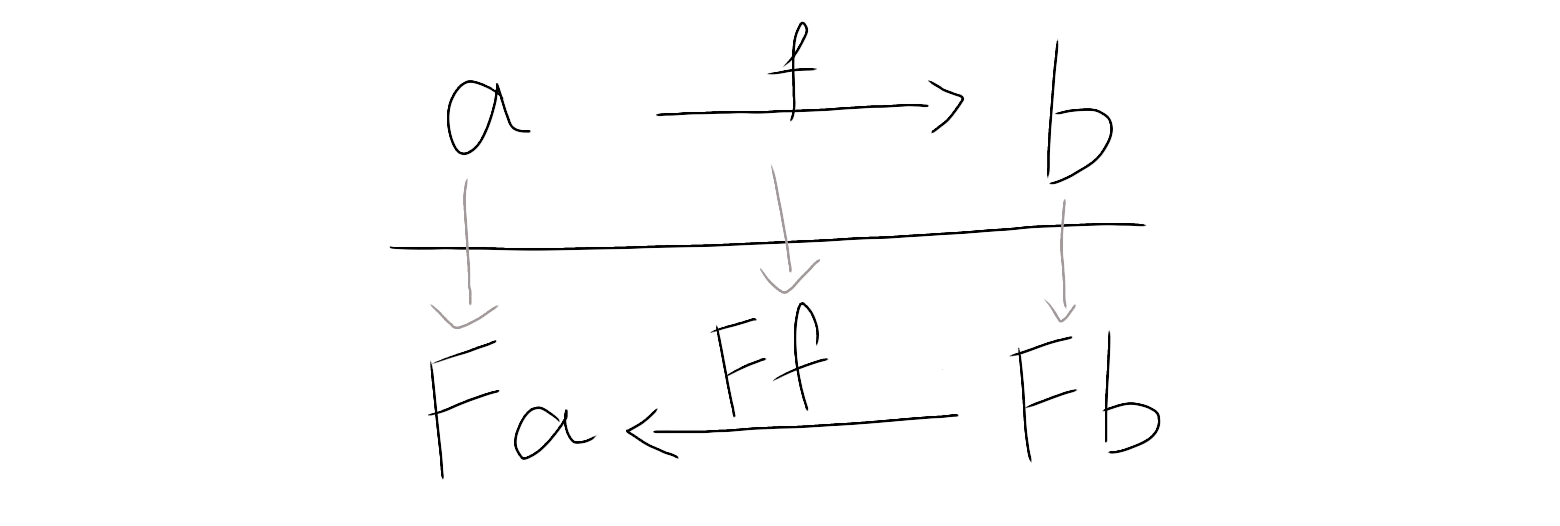
色々なFunctor
FunctorとContravariant
class Functor f where
fmap :: (a -> b) -> f a -> f b
class Contravariant f where
contramap :: (a -> b) -> f b -> f a
色々なFunctor
シンキング・タイム(10秒)
Contravariantになるような
データ構造を考えてみよう!
色々なFunctor
例1:関数
newtype Op b a = Op { runOp :: a -> b }
instance Contravariant (Op r) where
contramap f (Op g) = Op $ g . f
色々なFunctor
例2:Const
newtype Const a b = Const { getConst :: a }
instance Contravariant (Const r) where
contramap _ = Const . getConst
色々なFunctor
2つの関数を一つに束ねる
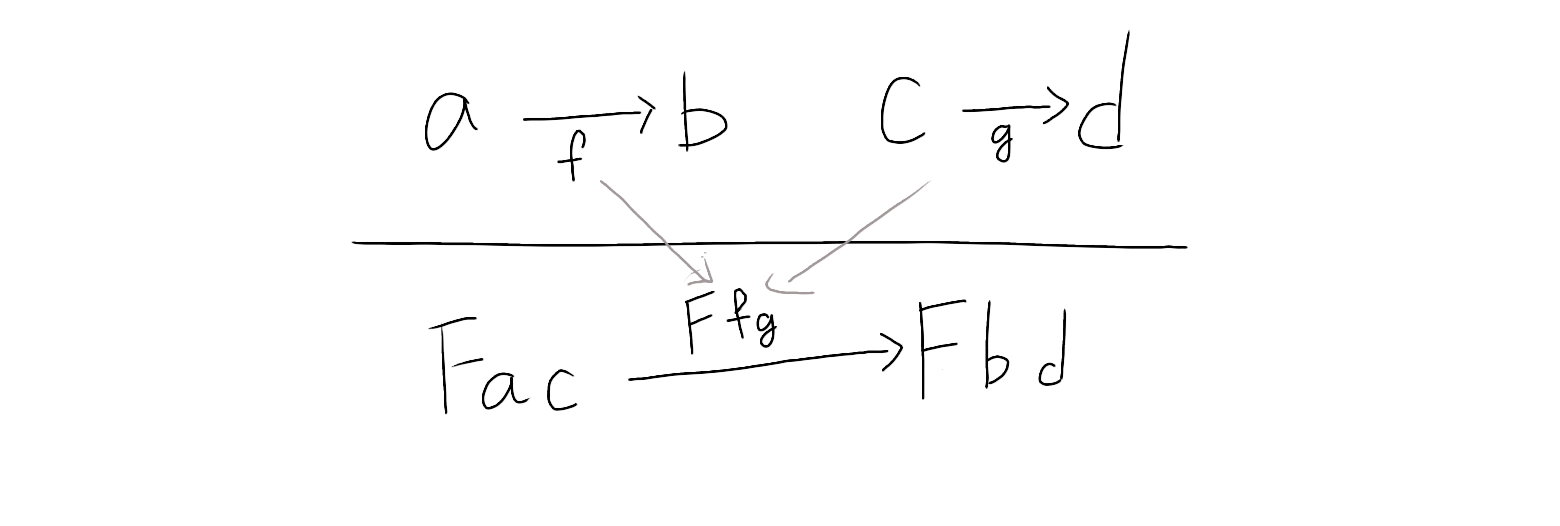
色々なFunctor
Bifunctor
class Bifunctor f where
bimap :: (a -> b) -> (c -> d) -> f a c -> f b d
first :: (a -> b) -> f a c -> f b c
first f = bimap f id
second :: (b -> c) -> f a b -> f a c
second f = bimap id f
色々なFunctor
Bifunctorの例:タプル、Const 等
instance Bifunctor (,) where
bimap f g (x, y) = (f x, g y)
instance Bifunctor Const where
bimap f _ (Const x) = Const $ f x
色々なFunctor
Bifunctorの矢印を片方だけ反転
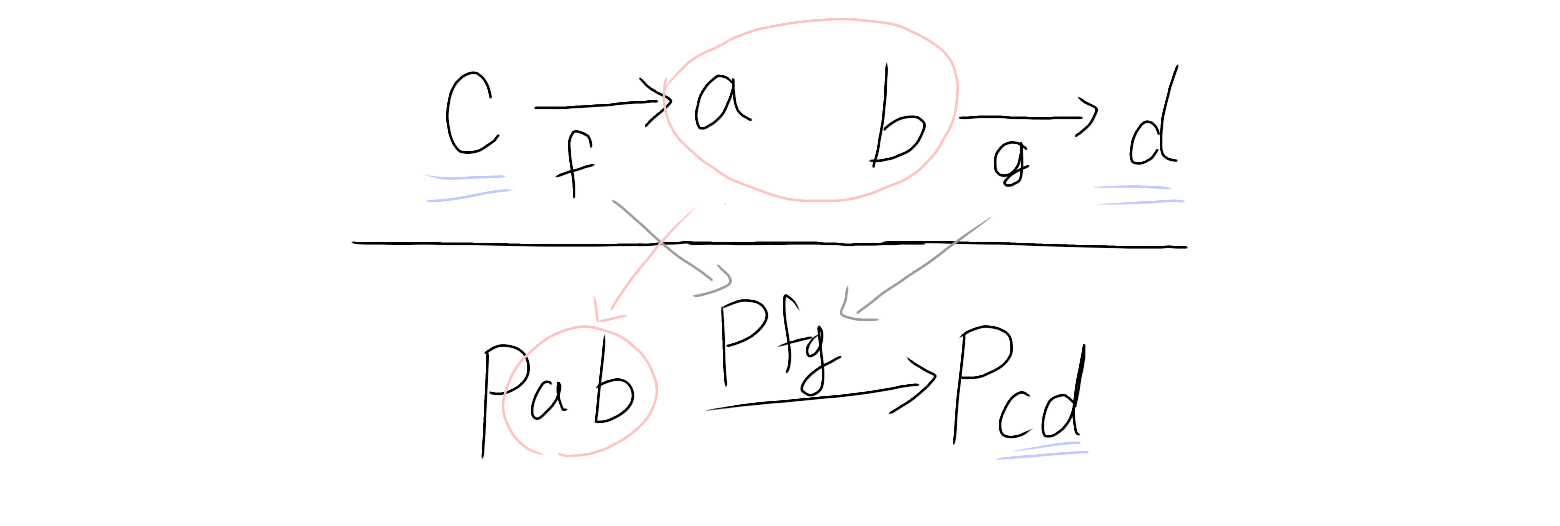
色々なFunctor
Profunctor
class Profunctor p where
dimap :: (c -> a) -> (b -> d) -> p a b -> p c d
lmap :: (a -> b) -> p b c -> p a c
lmap f = dimap f id
rmap :: (b -> c) -> p a b -> p a c
rmap = dimap id
色々なFunctor
矢印で表せるような、合成可能な構造は、
Profunctorになり得る。
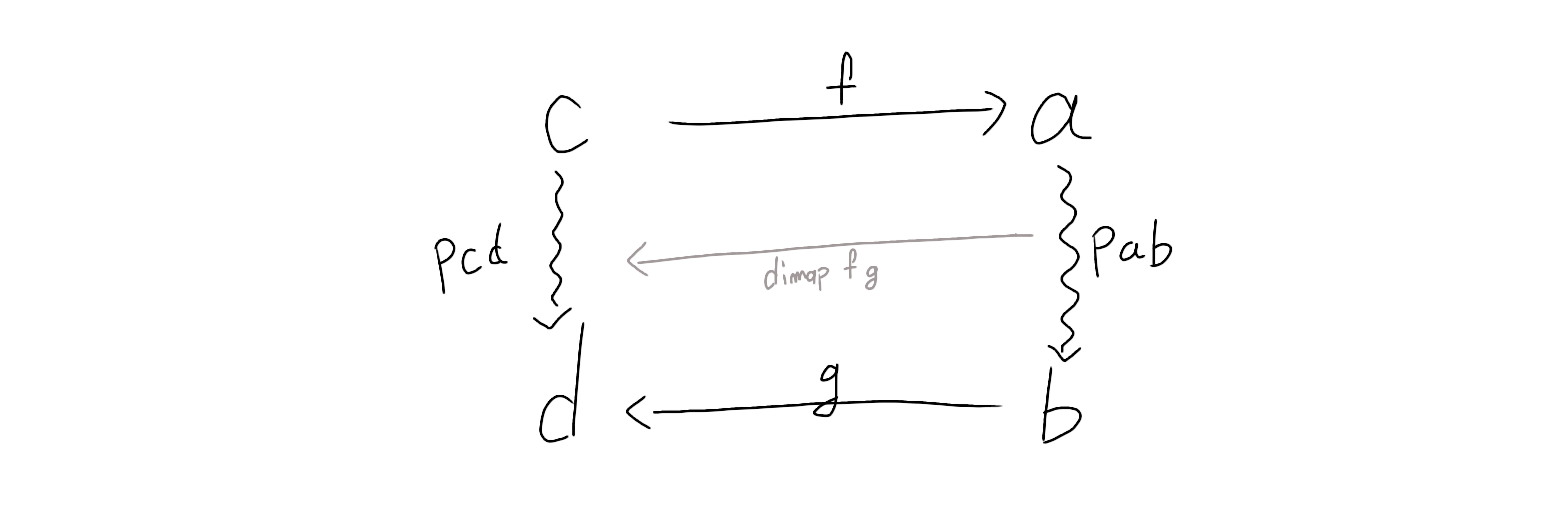
Lens, Optic, Prism
Lens, Optic, Prism
Lensの定義を再掲
type Lens s t a b
= forall f. Functor f => (a -> f b) -> s f t
Lens, Optic, Prism
Functorの制約を外す
type LensLike f s t a b = (a -> f b) -> s -> f t
これ以上の多相化は出来ない?
Lens, Optic, Prism
シンキング・タイム(10秒)
type LensLike f s t a b = (a -> f b) -> s -> f t
まだ抽象化出来る?
Lens, Optic, Prism
Haskellでは関数も型コンストラクタ
type LensLike f s t a b = (->) a (f b) -> (->) s (f t)
type Optic p f s t a b = p a (f b) -> p s (f t)
合成出来るように中央の(->)は残しておく
Lens, Optic, Prism
Prismの定義
type Prism s t a b = forall p f.
(Choice p, Applicative f) => p a (f b) -> p s (f t)
Lens, Optic, Prism
Choice型クラス?
後でまた詳しく説明します。
class Profunctor p => Choice p where
left' :: p a b -> p (Either a c) (Either b c)
left' = dimap (either Right Left) (either Right Left) . right'
right' :: p a b -> p (Either c a) (Either c b)
right' = dimap (either Right Left) (either Right Left) . left'
instance Choice (->) where
left' f (Left x) = Left $ f x
left' _ (Right x) = Right x
Lens, Optic, Prism
LensもPrismもOpticで表現出来る。
type Lens s t a b
= forall f. Functor f => Optic (->) f s t a b
type Prism s t a b
= forall p f. (Choice p, Applicative f) => Optic p f s t a b
Lens, Optic, Prism
実際のlensライブラリでは、
Opticをさらに多相にしたOpticalも定義されている
type Optical p q f s t a b = p a (f b) -> q s (f t)
type Optic p f s t a b = Optical p p f s t a b
Opticで全体を見渡す
Opticで全体を見渡す
ekmett/lensのアクセサはすべて、
Optic型に属し、(.)で合成出来る
type Optic p f s t a b = p a (f b) -> p s (f t)
pとfに様々な制約を与える事で
様々なアクセッサを、体系的に扱う。
Opticで全体を見渡す
- Opticベースのlensなら・・・
- 合成について明示的に定義しなくて良い
- lensモジュールに依存せずにアクセサを提供できる
- Haskellの文法に適した記法が得られる
- 定式化/分析がしやすそう
- 恋人が出来る
- お金持ちになれる
- etc.. etc..
Opticで全体を見渡す
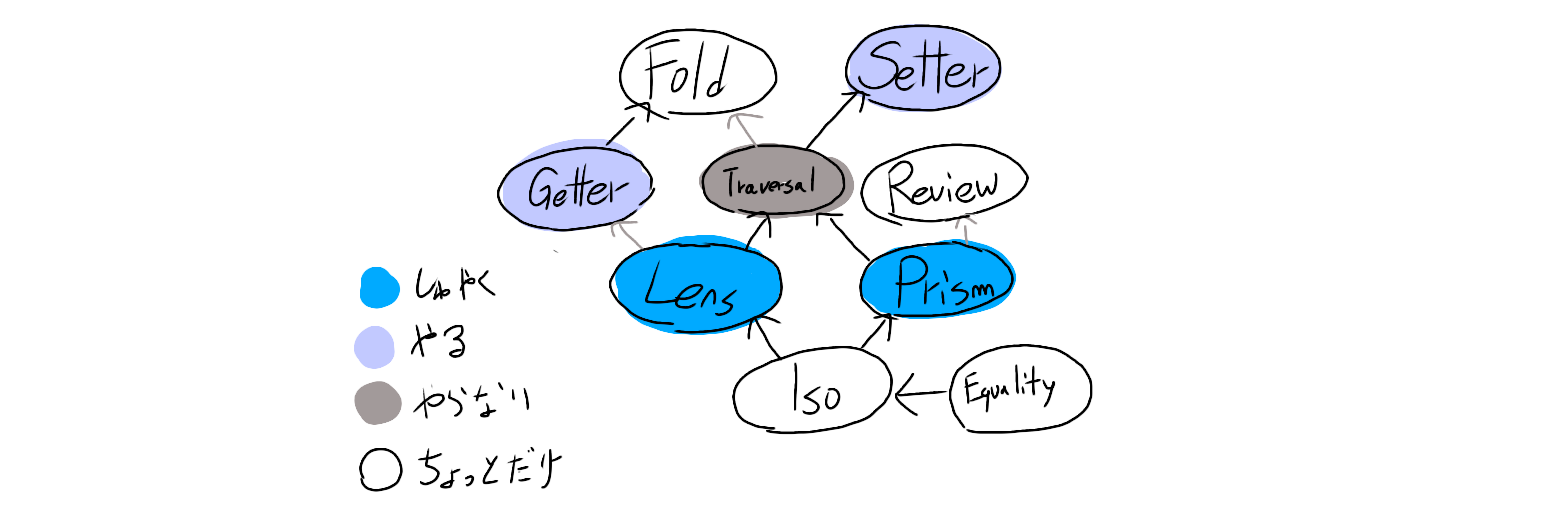
ekmett/lensに定義されている、
Lensの仲間をざっと見ていこう。
Opticで全体を見渡す
Equalityは、
pとfに任意の型を取れるようにしたもの。
a=b, s=tを表す。(つまり何も変換出来ない)
type Equality s t a b = forall p f. )ptic p f s t a b
type Equality' s a = Equality s s a )
id :: Equality a b a b
:: forall p f. p a (f b) -> p a (f b)
Opticで全体を見渡す
同型を表すIsoは、以下のように定義される。
type Iso s t a b
= forall p f. (Profunctor p, Functor f) => Optic p f s t a b
type Iso' s a = Iso s s a a
s=a, t=bでGetterになるため
通常Iso'の方を使う事になる。
Opticで全体を見渡す
iso関数を使えば簡単にIsoが作れるが、
変換が同型射である事は実装者が保証する。
iso :: (s -> a) -> (b -> t) -> Iso s t a b
iso f g = dimap f (fmap g)
boolMaybe :: Iso' Bool (Maybe ())
boolMaybe = iso bm mb
where
bm :: Bool -> Maybe ()
mb :: Maybe () -> Bool
Opticで全体を見渡す
from関数はIsoの向きを逆にする。
尚、ExchangeはProfunctor、IsoはAnIsoになる。
data Exchange a b s t = Exchange (s -> a) (b -> t)
instance Profunctor (Exchange a b) where
dimap f g (Exchange h i) = Exchange (h . f) (g . i)
type AnIso s t a b = Optic (Exchange a b) Identity s t a b
from :: AnIso s t a b -> Iso b a t s
Opticで全体を見渡す
IsoをGetterとして使う例。
もちろん、問題なくSetterにもなる。
(True, 10)^._1.boolMaybe -- Just ()
(False, 10)^._1.boolMaybe -- Nothing
(Just (), 10)^._1.from boolMaybe -- True
(Nothing, 10)^._1.from boolMaybe -- False
Opticで全体を見渡す
Isoのp::Profunctorを(->)に固定するとLens。
p::ProfunctorをChoiceにし、
f::FunctorをApplicativeにすればPrismになる。
type Lens s t a b
= forall f. Functor f => Optic (->) f s t a b
type Prism s t a b
= forall p f. (Choice p, Applicative f) => Optic p f s t a b
Opticで全体を見渡す
Prismから、a=t, f=bとして、
pにBifunctor制約を追加、fの制約をSettableに
type Review t b = forall p f.
(Choice p, Bifunctor p, Settable f) => Optic p f t t b b
尚、Settableは要Functor(後述)なので、
PrismはReviewになる。
Opticで全体を見渡す
TaggedはChoiceでありBifunctor
かつIdentityはSettableなので、
ReviewはAReviewになる、PrismもAReview
newtype Tagged t a = ...
instance Bifunctor Tagged where
instance Choice Tagged where
instance Settable Identity where
type AReview t b = Optic' Tagged Identity t b
Opticで全体を見渡す
Reviewを扱う関数。
可能な限り多相化されてるのでわかりづらい。
unto :: (Profunctor p, Bifunctor p, Functor f)
=> (b -> t) -> Optic p f s t a b
un :: (Profunctor p, Bifunctor p, Functor f)
=> Getting a s a -> Optic p f a a s s
re :: Contravariant f => AReview t b -> LensLike f b b t t
Opticで全体を見渡す
だいたいこんな感じ
unto :: (b -> t) -> Review s t a b
un :: Getter s a -> Review a a s s
re :: Review t t b b -> Getter b t
re関数でGetterに出来る。
てか、Getterにしないと何もできない。
Opticで全体を見渡す
やたら多相化されてるGetting/Getter
type Getting r s a = Optic (->) (Const r) s s a a
type Getter s a = forall f.
(Functor f, Contravariant f) => Optic (->) f s s a a
Const r は Contravariant(後述)なので、
GettingはGetterになる。
Opticで全体を見渡す
SetterはIdentityが多相化されていて、
Settable型クラスになっている。
type Setter s t a b
= forall f. Settable f => Optic (->) f s t a b
Opticで全体を見渡す
a=t, f=b に固定、fがContravariantかつApplicative
type Fold s a = forall f.
(Contravariant f, Applicative f) => Optic (->) f s s a a
Getter, Traversalの制約を強くしたもの、
当然、LensもPrismもFoldになる。
Opticで全体を見渡す
以下の2つの演算子はFoldのためのもの。
((^..)の説明は割愛。)
(^..) :: s -> Getting (Endo [a]) s a -> [a]
(^?) :: s -> Getting (First a) s a -> Maybe a
Getting r s a の r に指定する型がモノイドなら
その型はFoldになる(後述)
Prismの原理
Prismの原理
- lensライブラリは巨大&複雑
- すべての機能を把握するのは超大変
- よく使うところから少しづつ掘り下げていこう
- 今回はPrism周りの仕組みを解説
Prismの原理
まずは、ChoiceとPrismを再掲
class Profunctor p => Choice p where
left' :: p a b -> p (Either a c) (Either b c)
left' = dimap (either Right Left) (either Right Left) . right'
right' :: p a b -> p (Either c a) (Either c b)
right' = dimap (either Right Left) (either Right Left) . left'
type Prism s t a b = forall p f.
(Choice p, Applicative f) => Optic p f s t a b
Prismの原理
Choiceの二大インスタンス
その1:関数
instance Choice (->) where
left' f (Left x) = Left $ f x
left' _ (Right x) = Right x
Prismの原理
Choiceの二大インスタンス
その2:Tagged
newtype Tagged t a = Tagged { unTagged :: a }
instance Bifunctor Tagged where
bimap _ f = Tagged . f . unTagged
instance Profunctor Tagged where
dimap _ f = Tagged . f . unTagged
instance Choice Tagged where
right' = Tagged . Right . unTagged
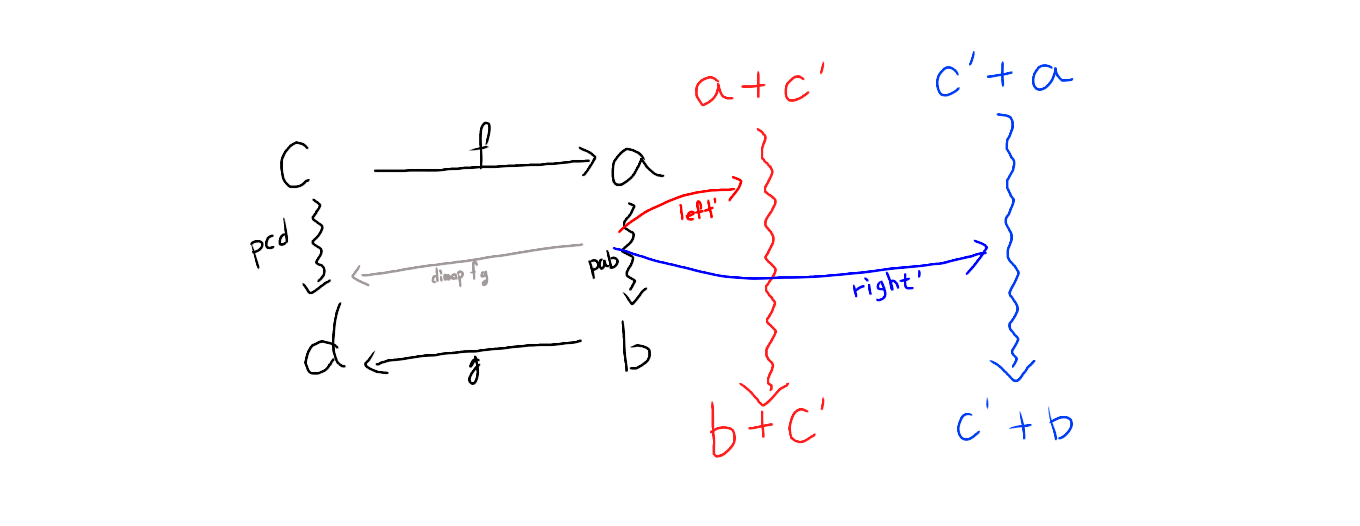
Prismの原理
ChoiceはProfunctorに別の変換を与える。
ちなみに、足し算はEitherを表す(圏論の慣習)
Prismの原理
Prismを作るためのprism関数
dimapとright'で順同型射からPrismを作れる
prism :: (b -> t) -> (s -> Either t a) -> Prism s t a b
prism bt seta = dimap seta (either pure $ fmap bt) . right'
_Just :: Prism (Maybe a) (Maybe b) a b
_Just = prism Just $ \case
Just x -> Right x
Nothing -> Left $ Nothing
Prismの原理
Setterの場合、over関数のタイミングで、
Optic p f s t a b の f が Identityに固定される
over :: Setter s t a b -> (a -> b) -> s -> t
over l f = getIdentity . l (Identity . f)
set :: Setter s t a b -> b -> s -> t
set a = over a . const
(.~) = set
Prismの原理
改めて、Setterの型と比較。
type Setter s t a b
= forall f. Settable f => Optic (->) f s t a b
type Prism s t a b = forall p f.
(Choice p, Applicative f) => Optic p f s t a b
関数はChoiceのインスタンスなので問題なし
Settableってなんだ。
Prismの原理
実はよくわかってない(´・ω・`)
けどIdentityはSettableのインスタンスなので、
pureとuntaintedがあればover相当の関数は作れるはず。
class Functor g => Distributive g where
distribute :: Functor f => f (g a) -> g (f a)
class (Applicative f
, Distributive f, Traversable f) => Settable f where
untainted :: f a -> a
instance Settable Identity where
untainted = getIdentity
Prismの原理
Prismアクセッサの動作を簡単にチェックしたい。
次のような型を作ってみよう。
data Hoge = Foo String | Bar Int | Buz String deriving Show
_Foo :: Prism Hoge Hoge String String
_Foo = prism Foo $ \case
Foo s -> Right s
x -> Left x
_Bar :: Prism Hoge Hoge Int Int
_Buz :: Prism Hoge Hoge String String
Prismの原理
f を Identityに固定する事で、
パターンにマッチした場合のみmap出来る事を、
次のようにして確認できる。
ghci> getIdentity . _Foo (Identity . (++"Piyo")) $ Foo "Hoge"
Foo "HogePiyo"
ghci> getIdentity . _Foo (Identity . (++"Piyo")) $ Bar 114514
Bar 114514
ghci> getIdentity . _Foo (Identity . (++"Piyo")) $ Buz "Hoge"
Buz "Hoge"
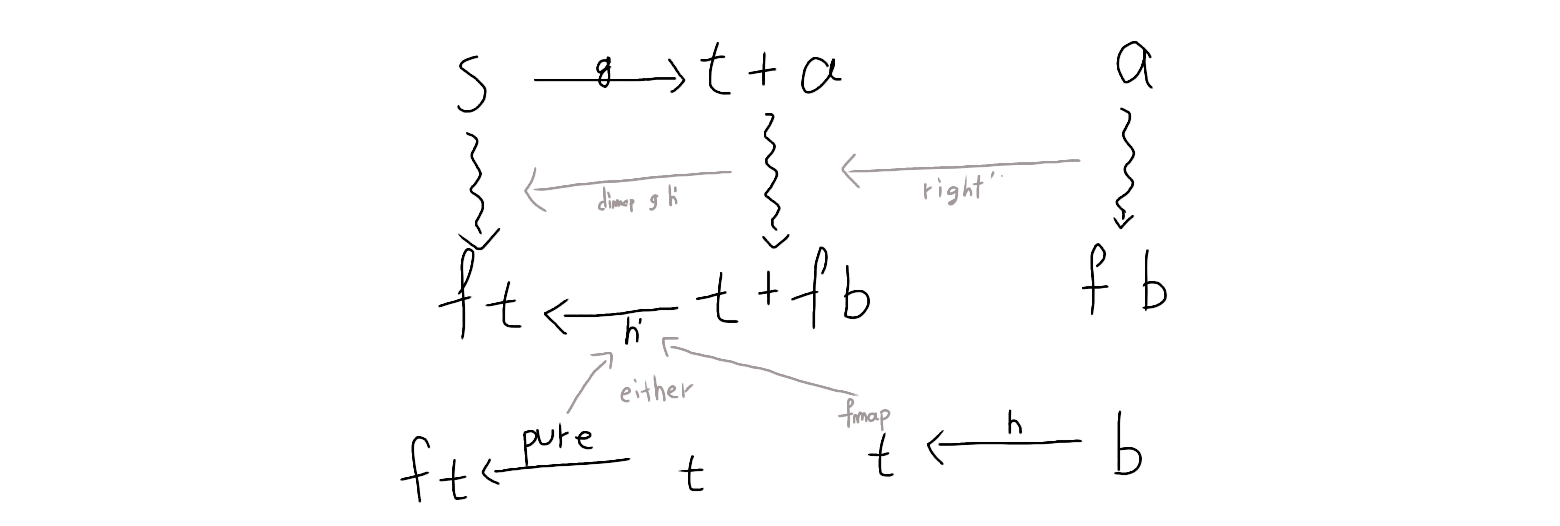
Prismの原理
以下のように図に描くとわかりやすい。
profunctor や f の型を固定して考えてみよう。
Prismの原理
Getterとして使う場合
Const r は Applicativeでない事に注意
type Prism s t a b =
forall p f. (Choice p, Applicative f) => Optic p f s t a b
type Getting r s a = Optic' (->) (Const r) s a
foldOf :: Getting a s a -> s -> a
foldOf l = getConst . l Const
(^.) = flip foldOf
Prismの原理
ただし、Gettingのrがモノイドの場合に限り、
Const rがApplicativeになる。
type Getting r s a = Optic' (->) (Const r) s a
instance Monoid m => Applicative (Const m) where
pure x = Const mempty
(<*>) _ = Const . getConst
Prismの原理
prism関数の定義を再掲
prism :: (b -> t) -> (s -> Either t a) -> Prism s t a b
prism bt seta = dimap seta (either pure $ fmap bt) . right'
マッチング出来ない場合は、
pureの部分でmemptyが取得される。
Prismの原理
Foldとして使う場合
ConstはContravariantになるので、
あとはFirst aがモノイドであればFoldになりそう。
type Fold s a = forall f.
(Contravariant f, Applicative f) => Optic' (->) f s a
type Getting r s a = Optic' (->) (Const r) s a
(^?) :: s -> Getting (First a) s a -> Maybe a
Prismの原理
FirstはMaybeと同型、
MaybeはMonoidになる。
newtype First a = First { getFirst :: Maybe a }
instance Monoid (First a) where
mempty = First Nothing
r@(First (Just )) `mappend` _ = r
First Nothing `mappend` r = r
Prismの原理
後はだいたいGetterの理屈と一緒
AccessingはGettingの変形
type Accessing p m s a = Optical p (->) (Const m) s s a a
foldMapOf :: Profunctor p => Accessing p r s a -> p a r -> s -> r
foldMapOf l f = getConst . l (Const #. f)
(^?) :: s -> Getting (First a) s a -> Maybe a
s ^? l = getFirst $ foldMapOf l (First #. Just) s
Prismの原理
re関数の実装、ようやくTagged登場
TaggedはChoice、IdentityはApplicativeの、
それぞれインスタンスなのでPrismはAReview
re :: Contravariant f => AReview t b -> LensLike f b b t t
re p = to (getIdentity #. unTagged #. p .# Tagged .# Identity)
newtype Tagged t a = Tagged { unTagged :: a }
type AReview t b = Optic' Tagged Identity t b
Prismの原理
prismの図を再掲、
re関数の動作原理を考えてみよう。

Prismの原理
直接コンストラクタを被せるのは、
簡単に試す事ができる。
純粋な関数になれば、to関数でGetterに出来る。
ghci> :t _Just $ Tagged (Identity 10)
_Just $ Tagged (Identity 10)
:: Num b => Tagged (Maybe a) (Identity (Maybe b))
ghci> getIdentity . unTagged . _Just $ Tagged (Identity 10)
Just 10
ghci> getIdentity . unTagged . _Foo $ Tagged (Identity "Hoge")
Foo "Hoge"
Prismの原理
reの実装は関数合成でも同じはず
(´・ω・`)あれ?
--これでも良いはず
re :: Contravariant f => AReview t b -> LensLike f b b t t
re p = to (getIdentity . unTagged . p . Tagged . Identity)
--実際
re :: Contravariant f => AReview t b -> LensLike f b b t t
re p = to (getIdentity #. unTagged #. p .# Tagged .# Identity)
-- ^ ^ ^ ^
-- why profunctor??
Prismの原理
Prismはただ単に順同型を表すので、
パターンマッチの用途に囚われず使える。
nat :: Prism' Integer Natural
nat = prism toInteger
$ \i -> if i < 0 then Left i else Right (fromInteger i)
5^?nat -- Just 5 :: Maybe Natural
(-5)^?nat -- Nothing :: Maybe Natural
(10 :: Natural)^.re nat -- 10 :: Integer
まとめ
まとめ
- Lensは便利
- でも直和型には弱い
- そんな時にはPrism!
- LensもPrismもOpticで表せるよ
- Opticでekmett/lens全体を見渡せる
- Prismの原理を覗いてみたよ
- Lens/Prismちょーすげぇ!